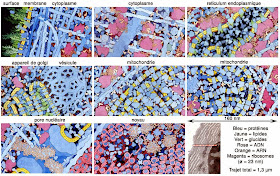
La figure suivante donne une idée assez exacte et à l’échelle de ce que verrait un être nanométrique lors d’un voyage dans le milieu intracellulaire depuis la membrane plasmique jusqu’au noyau d’une cellule eucaryote. On voit que les organites de la cellule s’empilent de manière extraordinairement compacte ne laissant aucun espace vide de taille nanométrique. Ce qui est surprenant c’est que malgré cet encombrement important tout ce qui est représenté ici ne montre que 1% du nombre total d’objets présents dans la cellule, le reste étant de l’eau à 99%.
Source: D. S. Goodsell, «The Machinery of Life», 2nd Ed., Springer, New-York (2009).
Il n’y a donc pas beaucoup de place pour bouger et la question se pose de savoir sous quelle forme se trouve l'eau intracellulaire qui représente quand même 70 pds% de la masse cellulaire. Pour cela rappelons que la masse molaire moyenne d’une protéine est de M = 40 kDa pour une densité moyenne de matière sèche de ρ = 1,35 g·cm-3 [1]. Le volume moyen d'une protéine isolée vaut donc:
\[{\rm{v}} = \frac{M}{{\rho \cdot{N_A}}} = \frac{{40000}}{{1,35 \times 0,60221413 \times {{10}^{24}}}} = 49,2 \times {10^{ - 21}}c{m^3}\]
ce qui correspond à une sphère de rayon R = 2,3 nm. La théorie cinétique des gaz nous apprend d'autre part que le diamètre d'une molécule d'eau subissant une choc thermique est voisin de 0,3 nm. L'idée est donc de supposer que, un peu à la manière d'un oignon, notre protéine s'entoure de plusieurs couches d'eau successives et le problème revient donc de savoir combien il faut de couches d'eau successives pour atteindre un taux d'hydratation voisin de 70 pds%. Or, si Vn le volume de la protéine recouverte de n couches d'eau, il en découle que le volume d'eau est (Vn - 50) et comme la densité de l'eau est proche de 1 g·cm-3, la masse d'eau vaut (Vn - 50)x1 tandis que la masse de protéine vaut 50x1,35, d'où la relation suivante reliant le pourcentage en masse au volume total Vn:
\[{V_n} = \frac{{4\pi }}{3}{\left( {2,3 + n \times 0,3} \right)^3} \Rightarrow \% {H_2}O({V_n}) = 100 \times \frac{{{V_n} - 50}}{{50 \times 1,35 + ({V_n} - 50)}} = \frac{{100 \times ({V_n} - 50)}}{{17,5 + {V_n}}}\]
Ainsi, si l’on ajoute une couche d’eau d’épaisseur 0,3 nm sur une protéine sèche de rayon 2,3 nm, on obtient un rayon de 2,6 nm correspondant à un volume d’eau de 74 - 50 = 24 nm3, soit un taux d’hydratation de 2400/(17,5+74) = 26 pds%. Avec une deuxième couche d’eau le rayon passe à 2,9 nm correspondant à un volume d’eau de 102 - 50 = 52 nm3, soit un taux d’hydratation de 5200/(17,5+102) = 44 pds%. Avec une troisième couche d’eau le rayon passe à 3,2 nm correspondant à un volume d’eau de 137 - 50 = 87 nm3, soit un taux d’hydratation de 8700/(17,5+137) = 56 pds%. Enfin, avec une quatrième couche d’eau le rayon passe à 3,5 nm correspondant à un volume d’eau de 180 - 50 = 130 nm3, soit un taux d’hydratation de 13000/(17,5+180) = 66 pds%. Avec une cinquième couche d'eau on aurait un taux d'hydratation trop élevé voisin de 73 pds%. Toute protéine globulaire se recouvre donc d'au plus 4 couches d’eau (soit une épaisseur de 4x0,3 = 1,2 nm), ce qui explique l'impossibilité de faire apparaître cette eau intracellulaire avec la même échelle que celle des organites.
Le calcul précédent ne concerne bien sûr que les protéines globulaires et il est donc légitime de se demander ce qu'il arriverait avec des protéines non sphériques. Si l'on suppose par exemple que le volume de 50 nm3 correspond en fait à un cylindre de rayon r = 1 nm et de longueur L = 16 nm et que l'on recouvre ce cylindre par une monocouche d'eau le rayon devient r = 1+0,3 = 1,3 nm pour une longueur L = 16+ 2x0,3 = 16,6 nm, soit un volume de 88 nm3, conduisant à un pourcentage d'eau de 100x(88-50)/(17,5+88) = 36 pds%. Avec cette nouvelle géométrie, il est facile de montrer que le taux de 70 pds% est atteint dès la troisième d'eau. Ceci est parfaitement logique dans la mesure où, à volume égal, un cylindre présente plus de surface qu'une sphère. En fait, il se trouve que pour un même volume de matière sèche, la forme sphérique est celle qui minimise le rapport surface sur volume et correspond donc à la forme qui nécessitera le nombre maximal de couches d'eau pour arriver à un taux d'hydratation de 70 pds%.
Il est également facile de refaire ce type de calcul pour le milieu extracellulaire. Par exemple, on sait que les biofilms sont des structures gélifiées constituées de polymères extracellulaires ayant une masse molaire moyenne de 180 kDa [2] pour une densité voisine 1,3 g·cm-3 [3] contenant environ 80 pds% d'eau. Modélisons ces polymères de volume V = 230 nm3 comme des cylindre de longueur L = 73 nm et de rayon R = 1 nm. Pour n couches d'eau ayant chacune une épaisseur de 0,3 nm le volume hydraté et le taux d'hydratation s'expriment comme:
\[{V_n} = \pi (73 + 2 \times 0,3 \times n) \times {\left( {1 + n \times 0,3} \right)^2} \Rightarrow \% {H_2}O({V_n}) = \frac{{100 \times ({V_n} - 230)}}{{230 \times 1,3 + ({V_n} - 230)}}\]
Comme on pourra aisément le vérifier, on obtient pour n = 5 un taux d'hydratation voisin de 81 pds%. Ceci démontre qu'une eau extracellulaire au contact de polymères linéaires présente a peu de choses près la même structure en 4-5 couches qu'une eau intracellulaire au contact de protéines globulaires.
Un calcul similaire peut aussi être fait pour les argiles qui présentent des structures en feuillets de type aluminosolicates présentant une épaisseur allant de 0,7 nm à 1,4 nm pour une densité voisine de 2,5 g·cm-3. Soit A l'aire du feuillet d'épaisseur h et n, le nombre de couches d'eau empilées de part et d'autre du feuillet. Le volume du feuillet anhydre est dans ces conditions V = A·e , ce qui conduit à la relation suivante:
\[{V_n} = A\cdot\left( {h + 0,6 \times n} \right) \Rightarrow \% {H_2}O({V_n}) = 100 \times \frac{{A\cdot0,6 \times n}}{{A\cdot h \times 2,5 + A\cdot 0,6 \times n}} = \frac{{60 \times n}}{{h \times 2,5 + 0,6 \times n}}\]
Pour une épaisseur h = 0,7 nm correspondant à une argile de type (1/1) comme une serpentine, on constate qu'il faut ainsi n = 7 couches d'eau pour atteindre un taux d'hydratation de 70% en masse tandis qu'il faudrait n = 14 couches pour un feuillet d'épaisseur h = 1,4 nm correspondant à une argile de type (2/1/1) comme une chlorite. On notera ici que l'aire A peut être quelconque et donc de dimension macroscopique. En revanche, il est crucial que l'épaisseur h soit nanométrique. En effet si l'on prend h = 1 000 000 nm = 1 mm, le même calcul donne n = 140 000, ce qui correspond à un eau liquide et non plus morphogénique.
Nous appellerons cette structuration en couches de l'eau autour de toute matière présentant au moins une dimension de type nanométrique "eau morphogénique" car il s'agit bel et bien d'un nouvel état physique de l'eau qui doit être identifié en tant que tel comme étant apte à donner une forme gélifiée, intermédiaire entre l'état liquide et l'état solide à des colloïdes minéraux ou organiques. On notera que l'aspect nanométrique Le tableau suivant compare les propriétés physique de l'eau liquide, de l'eau morphogénique et de la glace [4]:
Comme on peut le constater, les trois types d'eau sont foncièrement différentes. Ainsi l'eau morphogénique apparaît moins dense et nettement plus visqueuse que l'eau liquide mais reste plus dense que la glace. Elle surpasse l'eau liquide et la glace pour ce qui concerne la quantité d'énergie à apporter par échange thermique pour élever d'un kelvin la température de 1g d'eau, la dilatation thermique isobare, la compressibilité adiabatique ou la conductivité thermique. Si l'eau morphogénique relaxe moins vite que l'eau liquide et transporte moins bien les espèces ioniques, elle surclasse néanmoins très largement la glace pour ces propriétés de nature électrique. Enfin, si le son est plus absorbé par l'eau morphogénique que par l'eau liquide, cette absorption reste très faible par rapport à la glace.
Comme le montre la figure suivante, la diffusion inélastique des neutrons réalisée sur des membranes cellulaires ou de l’ADN confirme que l’eau morphogénique autour de ces structures biologiques n’a pas du tout la même structure, ni la même dynamique que la glace hexagonale [5]:
Il est également facile de refaire ce type de calcul pour le milieu extracellulaire. Par exemple, on sait que les biofilms sont des structures gélifiées constituées de polymères extracellulaires ayant une masse molaire moyenne de 180 kDa [2] pour une densité voisine 1,3 g·cm-3 [3] contenant environ 80 pds% d'eau. Modélisons ces polymères de volume V = 230 nm3 comme des cylindre de longueur L = 73 nm et de rayon R = 1 nm. Pour n couches d'eau ayant chacune une épaisseur de 0,3 nm le volume hydraté et le taux d'hydratation s'expriment comme:
\[{V_n} = \pi (73 + 2 \times 0,3 \times n) \times {\left( {1 + n \times 0,3} \right)^2} \Rightarrow \% {H_2}O({V_n}) = \frac{{100 \times ({V_n} - 230)}}{{230 \times 1,3 + ({V_n} - 230)}}\]
Comme on pourra aisément le vérifier, on obtient pour n = 5 un taux d'hydratation voisin de 81 pds%. Ceci démontre qu'une eau extracellulaire au contact de polymères linéaires présente a peu de choses près la même structure en 4-5 couches qu'une eau intracellulaire au contact de protéines globulaires.
Un calcul similaire peut aussi être fait pour les argiles qui présentent des structures en feuillets de type aluminosolicates présentant une épaisseur allant de 0,7 nm à 1,4 nm pour une densité voisine de 2,5 g·cm-3. Soit A l'aire du feuillet d'épaisseur h et n, le nombre de couches d'eau empilées de part et d'autre du feuillet. Le volume du feuillet anhydre est dans ces conditions V = A·e , ce qui conduit à la relation suivante:
\[{V_n} = A\cdot\left( {h + 0,6 \times n} \right) \Rightarrow \% {H_2}O({V_n}) = 100 \times \frac{{A\cdot0,6 \times n}}{{A\cdot h \times 2,5 + A\cdot 0,6 \times n}} = \frac{{60 \times n}}{{h \times 2,5 + 0,6 \times n}}\]
Pour une épaisseur h = 0,7 nm correspondant à une argile de type (1/1) comme une serpentine, on constate qu'il faut ainsi n = 7 couches d'eau pour atteindre un taux d'hydratation de 70% en masse tandis qu'il faudrait n = 14 couches pour un feuillet d'épaisseur h = 1,4 nm correspondant à une argile de type (2/1/1) comme une chlorite. On notera ici que l'aire A peut être quelconque et donc de dimension macroscopique. En revanche, il est crucial que l'épaisseur h soit nanométrique. En effet si l'on prend h = 1 000 000 nm = 1 mm, le même calcul donne n = 140 000, ce qui correspond à un eau liquide et non plus morphogénique.
Nous appellerons cette structuration en couches de l'eau autour de toute matière présentant au moins une dimension de type nanométrique "eau morphogénique" car il s'agit bel et bien d'un nouvel état physique de l'eau qui doit être identifié en tant que tel comme étant apte à donner une forme gélifiée, intermédiaire entre l'état liquide et l'état solide à des colloïdes minéraux ou organiques. On notera que l'aspect nanométrique Le tableau suivant compare les propriétés physique de l'eau liquide, de l'eau morphogénique et de la glace [4]:
Comme le montre la figure suivante, la diffusion inélastique des neutrons réalisée sur des membranes cellulaires ou de l’ADN confirme que l’eau morphogénique autour de ces structures biologiques n’a pas du tout la même structure, ni la même dynamique que la glace hexagonale [5]:
En effet, les vibrations d’élongation des liaisons hydrogène dans la glace sont observées à 28 meV (224 cm-1, liaisons faibles) et 37 meV (296 cm-1, liaisons fortes) tandis que les mouvements de libration donnent une bande large entre dans la gamme 67-121 meV (536-968 cm-1). Pour l’eau entourant l’ADN à T < 30 K, on constate qu’en dessous d’une teneur en eau de 33 pds% tous les pics caractéristiques de la glace sont absents et l’on observe qu’un seul signal large qui démarre à 54 meV (296 cm-1) et culmine à 73 meV (584 cm-1). Le même phénomène est observé pour les membranes qui présente des modes de vibrations très différents de ceux de la glace hexagonale. On constate aussi une certaine similitude avec l'eau hydratant l'ADN au dessus de 50 meV associée à une nette différence en dessous de 50 meV.
Nous pouvons donc retenir que, sur un plan topologique, un être vivant est donc fait à plus de 99% d’eau qui existe sous un état qui n'est ni solide, ni liquide, appelé «eau morphogénique», ayant ses caractéristiques thermodynamique propres liées à la formation d'une gaine d’eau ayant une épaisseur d’au plus 5 couches d’eau et enrobant toute matière biologique. Comme l'exprime si bien Albert Szent-Györgyi, «La vie c’est de l’eau dansant sur la mélodie des solides» [6]. On pourrait aussi citer Sir Oliver Lodge, «Imaginez un poisson des profondeurs au fond de l’océan. Il est entouré d’eau, il vit dans l’eau et il respire dans l’eau. Maintenant, posons nous la question de savoir la dernière chose que ce poisson pourra découvrir. J’ai tendance à penser que cette ultime chose que le poisson pourra découvrir sera l’eau...» [7]. L'eau morphogénique pourrait donc bien être un quatrième état de la matière identifié en tant que tel dès 1931 par Sir William Hardy, spécialiste du problème de la lubrification des surfaces [8].
Références
[1] Quillin M. L., Matthews B. W., «Accurate calculation of the density of proteins», Acta Cryst. D, 56 (2000) 791-794.
[2] Ras M., Lefebvre D., Derlon N., Paul E., Girbal-Neuhauser E., «Extracellular polymeric substances diversity of biofilms grown under contrasted environmental conditions», Water Research, 45 (2011) 1529-1538.
[3] Melo L.F., «Biofilm physical structure, internal diffusivity and tortuosity», Water Science & Technology, 52 (2005) 77–84.
[4] Pollack G. H., «Cells, Gels and the Engines of Life», Ebner & Sons, Seattle (2001) pp. 73.
[5] Ruffle S. V., Michalarias. I., Li J.-C., Ford R.C., «Inelastic neutron scattering studies of water interacting with biological membranes», J. Am. Chem. Soc., 124 (2002) 565-569.
[6] A. Szent-Györgyi, «The living state with observations on cancer», Academic Press, New York (1972) p. 9.
[7] «Lodge pays tribute to Einstein theory», New York Times, 9 février 1920.
[8] W. Hardy, «Problems of the boundary state», Phil. Trans. R. Soc. Lond. A, 230 (1932) 1-37.
[2] Ras M., Lefebvre D., Derlon N., Paul E., Girbal-Neuhauser E., «Extracellular polymeric substances diversity of biofilms grown under contrasted environmental conditions», Water Research, 45 (2011) 1529-1538.
[3] Melo L.F., «Biofilm physical structure, internal diffusivity and tortuosity», Water Science & Technology, 52 (2005) 77–84.
[4] Pollack G. H., «Cells, Gels and the Engines of Life», Ebner & Sons, Seattle (2001) pp. 73.
[5] Ruffle S. V., Michalarias. I., Li J.-C., Ford R.C., «Inelastic neutron scattering studies of water interacting with biological membranes», J. Am. Chem. Soc., 124 (2002) 565-569.
[6] A. Szent-Györgyi, «The living state with observations on cancer», Academic Press, New York (1972) p. 9.
[7] «Lodge pays tribute to Einstein theory», New York Times, 9 février 1920.
[8] W. Hardy, «Problems of the boundary state», Phil. Trans. R. Soc. Lond. A, 230 (1932) 1-37.



Aucun commentaire:
Enregistrer un commentaire